Transformations
Cubic Polynomials
Odd polynomials have some similarities to quadratic transformation as well, but with some differences. The simplest case is the cubic function. Cubic functions can be sketched by transformation if they are of the form f (x) = a(x - h)3 + k, where a is not equal to 0. Note that this form of a cubic has an h and k just as the vertex form of a quadratic. However, this does not represent the vertex but does give how the graph is shifted or transformed. The horizontal shift is given by the h. The vertical shift is given by the k.
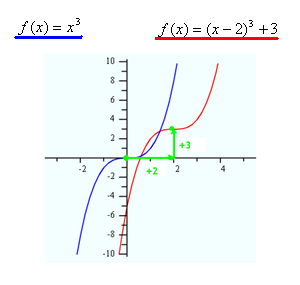
The simplest cubic function, or parent function, is f(x) = x3, where a = 1 and both h and k = 0, as in f(x)=1(x - 0)3 + 0. How is the parent function transformed if the function becomes f( x) = (x - 2)3 + 3? The parameters a, h, and k are 1, 2, and 3, respectively. These parameters make the graph of the standard function, f(x) = x3, shifted 2 units right and 3 units up, as you can see below: