Factoring
When a is not 1
Area Model Method
Example Factor and solve 2x2 + x - 6 = 0 (same equation from last example).
After following steps 1 - 3 in the previous example, the factor pair needed is -3 and 4. At this point the rest of the steps will be based on the area model.
Step 4. Enter the first and last terms into the area model in the upper left and lower right squares.
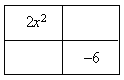
Step 5. Enter the factor pair determined earlier into the other two squares. Because of the Commutative Property of Multiplication, it does not matter which factor is put in which square.

Step 6. Factor the GCF from each row and column and write them on the outside of the box.

Step 7. The two terms across the top create one binomial and the two terms along the left-hand side create the other binomial. The factored form is:
(2x - 3)(x + 2) = 0
Step 8. Use the Zero Product Property to set each factor equal to zero and solve.
2x - 3 = 0 or x + 2 = 0
x = 1.5 or x = -2