Standard Form
Introduction
The standard form of a quadratic equation is ax2 + bx + c = 0 where a, b, and c are real numbers and a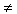 0. Earlier in this unit, vertex form and factored form were discussed. There is a similarity between all three forms. The "a" in the standard form is the same "a" as in the factored and vertex form. That is, the a will always have exactly the same value. To determine the values of a, b, and c, write the equation in standard form.
0. Earlier in this unit, vertex form and factored form were discussed. There is a similarity between all three forms. The "a" in the standard form is the same "a" as in the factored and vertex form. That is, the a will always have exactly the same value. To determine the values of a, b, and c, write the equation in standard form.
Example 1 Find the a, b, and c values of the equation: x2 - 3x = 28.
Step 1. Put the equation in standard form.
1x2 - 3x - 28 = 0
Step 2. Identify the a, b, and c values.
a = 1, b = -3, c = -28
Example 2 Find the a, b, and c values of the equation: 5x2 = -45.
Step 1. Put the equation in standard form.
5x2 + 0x + 45 = 0
Step 2. Identify the a, b, and c values.
a = 5, b = 0, c = 45