Factor by Grouping
Factoring
By Grouping
When polynomials have an even number of terms, sometimes they can be factored by grouping. The example below will demonstrate how to factor by grouping.
Example Factor and solve the following polynomial:
![]()
Step 1. Use parentheses to group the terms into equal groups.
![]()
Step 2. Factor the GCF from each group.
![]()
Step 3. Since the two remaining factors are both (x + 3), use Distributive Property to regroup.
![]()
Step 4. Use Zero Product Property to solve the polynomial.
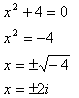 or
or ![]()
*Note: Since only one of these solutions is a real number, there is only one x -intercept on the graph of the corresponding function.