Using Square Roots
| Site: | St. Louis |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Using Square Roots |
| Printed by: | Guest user |
| Date: | Sunday, April 28, 2024, 3:47 PM |
Description
Using Square Roots
Number of Solutions
The standard form of a quadratic equation is: ax2 + bx+c = 0. Solving quadratic equations will result in two, one or no real solutions. Since a quadratic equation contains a squared term, square roots will be needed to find solutions. Remember that the square root of a positive number produces a positive and negative answer. For example,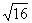 
= 4 and -4, since 42 = 16 and (-4) 2 = 16. This situation creates the two solution scenario. When taking the square root of zero, there is only one answer, 0. This situation creates the one solution scenario. When taking the square root of a negative number, an imaginary number is needed. For example, 
. This situation creates the no real solution scenario.
= 4 and -4, since 42 = 16 and (-4) 2 = 16. This situation creates the two solution scenario. When taking the square root of zero, there is only one answer, 0. This situation creates the one solution scenario. When taking the square root of a negative number, an imaginary number is needed. For example, 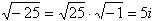. This situation creates the no real solution scenario.Example 1
Solve the equation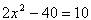 
using square roots.
using square roots. Step 1. Isolate the x2 -term.
Step 2. Take the square root of both sides.
*Note:x = 5 or -5 are the two solutions to the equation. They are also the x -intercepts of the graph.
Example 2
Solve the equation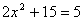 
using square roots.
using square roots. Step 1. Isolate the x2 -term.
Step 2. Take the square root of both sides.
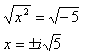
Video Lesson
To learn how to solve quadratic equations by using square roots, select the following link:
Guided Practice
To solidify your understanding of solving quadratics using square roots, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Guided Practice
Guided Practice
Practice
Solve by Square Roots Worksheet
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Answer Key
Solve by Square Roots Answer Key
*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,†refresh your browser.
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Quadratic Equations and Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch09_07_homeworkhelp.html (accessed 7/22/2010).
Kuta Software, www.kutasoftware.com/free.html (accessed 07/22/2010).