Graphical Behavior
| Site: | St. Louis |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Graphical Behavior |
| Printed by: | Guest user |
| Date: | Saturday, March 7, 2026, 9:48 PM |
Description
Introduction
When graphing polynomials, there are important characteristics to consider such as: behavior at the ends of the graph, location of the relative minimum and maximum points, and the zeros of the function. A sketch of the graph can be determined by looking at the equation when you have an understanding of these important characteristics. These key parts of the polynomial will be discussed in the following sections.
Graphs of Polynomials
When graphing a polynomial, the number of different real roots is the number of times the polynomial crosses the x-axis. A root is the place where the polynomial meets the x-axis. At the x-axis, the value of y is always zero. Other names for roots are solutions, x-intercepts, and zeros.
Starting with a polynomial of degree 1, this is a straight line that will cross the x-axis 1 time. The sign of the coefficient of x tells us if the line will be rising or falling as it runs from left to right. When a polynomial is of degree 2, its graph forms a parabola. The coefficient of the x2 term now determines if the parabola will open up or down. These functions have been discussed in earlier units.
The next one is a third degree polynomial. Again, the leading coefficient, which in this case is the x3 term, determines which way the graph will point. If it is positive, then the graph will go from the lower left corner to the upper right corner of the grid, while a negative coefficient will give a graph going from the upper left corner to the lower right corner of the grid.
Examples
Here is an example of a third degree polynomial with three real roots and a positive leading coefficient.
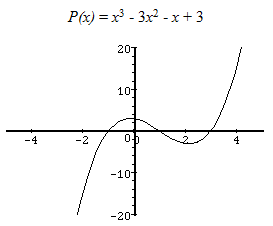
Below is a polynomial with two real roots and a negative leading coefficient. Notice that even though this is a cubic equation, there are only two real roots. The rule states that a cubic can have at most three real roots, but it can have less than three. The other roots will be represented by imaginary numbers.
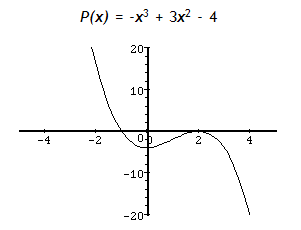
Looking for Patterns
There are patterns in the graphs of the previous examples. If the degree is odd, the polynomial will have at least one real root and up to as many as the degree of the polynomial. For example, if the degree of the polynomial is five, there can be as few as one or as many as five real roots or x-intercepts.
The leading coefficient determines whether the graph is going from lower left to upper right or from upper left to lower right on the graph. When the polynomials have an even degree, say of degree n, the graph has anywhere from 0 to n real roots. Here the leading coefficient determines whether the graph points up (if it is positive) or down (if it is negative). So by plotting the real roots and using these two "rules", we have an idea of what the graph of the polynomial looks like.
Graphs of polynomials have no holes or breaks in the graph and no sharp corners, are always nice smooth curves. The "humps" where the graphs change direction from increasing to decreasing or decreasing to increasing are often called turning points. If the polynomial has degree n then there will be at most n - 1![]() turning points in the graph. Therefore, a fourth degree polynomial will have no more than 3 turning points.
turning points in the graph. Therefore, a fourth degree polynomial will have no more than 3 turning points.
Example 1
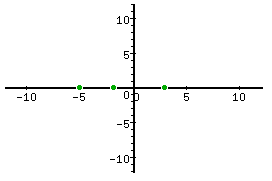
Graph the polynomialp(x) = (x - 3)(x + 2)(x + 5).
Step 1. Plot the roots as x-intercepts.
In the polynomial, p(x) = (x - 3)(x + 2)(x + 5), the roots are 3, -2, and -5.
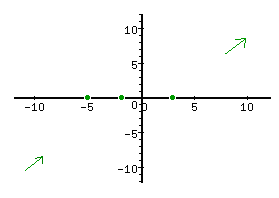
Step 2. Use the leading coefficient to determine the end behavior.
To find the coefficient, multiply the factors and get x3 + 4x2 - 11x - 30. Or just multiply the x-terms, in this case, (+x)(+x)(+x) which multiplies to (+x3).
The leading coefficient is positive 1, which implies the graph will go from bottom left to upper right.
Step 3. Substitute the value x = 0, find the value of y.
The point (0,-30) is on the graph and will help in creating the curve. The sketch of the graph is:
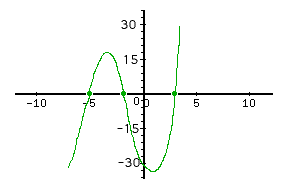
*Note: Since this is only a sketch, ALL data may not be exact.
Example 2
Graph the polynomial p(x) = (-x + 2)(x2 + 5).
Step 1. Plot the real roots.
Set each factor equal to zero to find the roots.
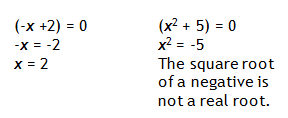
Therefore, there is only one real root and that is x = 2.
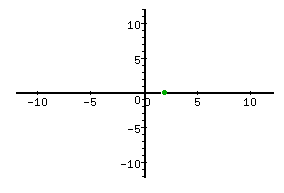
Step 2. Use the leading coefficient to determine the end behavior.
Multiply the polynomial to get -x3 + 2x2 - 5x + 10 or (-x)(x2) to find that the leading coefficient is -1.
Therefore the graph goes from upper left to lower right.
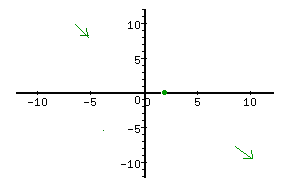
Step 3. Substitute the value x = 0, find the value of y.
This calculation produces the point (0, 10).
Combining this bit of information, the sketch of the graph could look like:
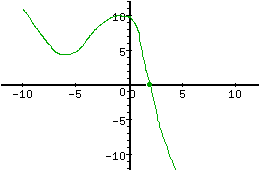
*Note: With the information given, it is not possible to determine the exact shape of the graph. This graph is an approximation.
Exploration
Building Polynomials Worksheet
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
End Behavior
When graphing polynomials, it can help to have an idea of what basic polynomial shapes look like. One of the aspects of this is the graph's end behavior, or the behavior of the graph of the polynomial when the "x" values get either very large or very small (the right and left sides of the graph). Look at the following graphs to see examples of end behavior.
Even Degree
Even-degree polynomials either open up (if the leading coefficient is positive) or down (if the leading coefficient is negative). All even-degree polynomials behave, on their ends, like quadratics.
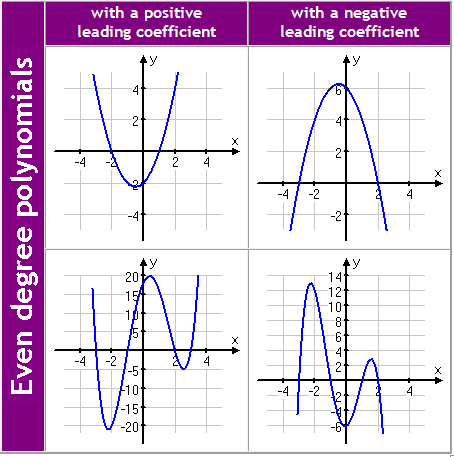
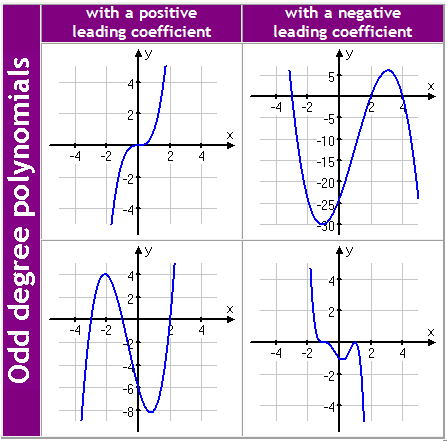
Odd Degree
Odd-degree polynomials have ends that head off in opposite directions. If they start lower left and go to upper right, they're positive polynomials; if they start upper left and go down to lower right, they're negative polynomials. All odd-degree polynomials behave, on their ends, like cubics.
Example 1
Which of the following could be the graph of a polynomial whose leading term is "-3x4"?
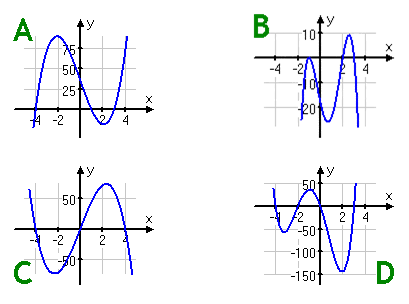
Step 1. Consider the degree.
The exponent says that this is a 4th degree polynomial, so the graph will behave roughly like a quadratic (up on both ends or down on both ends).
Step 2. Consider the leading coefficient.
Since the sign on the leading coefficient is negative, the graph will be down on both ends.
Step 3. Pick a graph.
Based on end behavior, graph B is correct.
Example 2
Describe the end behavior of f(x) = 3x7 + 5x + 1004.
Step 1. Consider the degree.
The exponent says that this is a 7th degree polynomial, so the graph will behave roughly like a cubic: the ends will point in opposite directions.
Step 2. Consider the leading coefficient.
Since the sign on the leading coefficient is positive, the graph will be increasing from lower left to upper right.
Summary
The end behavior of polynomials is as follows:
For even degree polynomials, with a positive leading coefficient,
- as x approaches infinity, f(x) or y approaches infinity
- and as x approaches negative infinity, f(x)or y approaches infinity
For odd degree polynomials, with a positive leading coefficient,
- as x approaches infinity, f(x) approaches infinity
- and as x approaches negative infinity, f(x) approaches negative infinity
Polynomials with negative leading coefficients will have the opposite end behaviors. For example, odd degree polynomials with a negative leading coefficient,
- as x approaches infinity, f(x) approaches negative infinity
- and as x approaches negative infinity, f(x) approaches positive infinity
Interactive Activity
To learn more about even and odd functions, select the following link:
Practice
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Maximum & Minimum
From previous sections, graphs of 2nd degree polynomials are parabolas. Depending on whether they open upward or downward, they will have a maximum or minimum point. Polynomials of degree greater than 2 can have more than one maximum or minimum value. The largest possible number of minimum or maximum points is one less than the degree of the polynomial. The following examples illustrate several possibilities.
Example 1
An even polynomial of degree higher than two will open up or down, but may contain more than one curve. Notice this case of y = x4 + 3x 3 + 4.
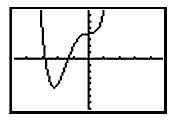
The minimum is located at x = -2.25 and the minimum value is approximately -4.54. There is only one minimum and no maximum point. The value -4.54 is the absolute minimum since no other point on the graph is lower.
Example 2
Let P(x) = -x6 - 3x3 + x + 1.
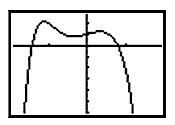
There are two maximum points at (-1.11, 2.12) and (0.33, 1.22). There is a minimum at (-0.34, 0.78). The maximum value of 2.12 at x = -1.11 is the absolute maximum since no point on the graph is higher. The maximum value of 1.22 at x = 0. 33 is called a relative maximum, being the largest value "relative" to points close to it on the graph. The minimum value of 0 .78 at x = -0.34 is a relative minimum, being the smallest value "relative" to points close to it on the graph.
Example 3
An odd polynomial of degree higher than three will look much like a cubic, and may contain more than one curve. Since odd functions have opposite end behavior, there is never an absolute maximum or minimum.
Let P(x) = -2x3 + 7x2 - 3x.
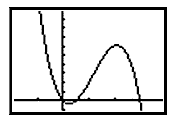
There is a relative minimum value of -0.34 at approximately x = 0.24 and a relative maximum value of 6 .05 at approximately x = 2.09.
Calculator Instructions
To locate the maximum or minimum points by using the TI-83/84 calculator, use the ![]() buttons to open the "Calc" menu and the "3. minimum" or "4. maximum" functions to calculate these values.
buttons to open the "Calc" menu and the "3. minimum" or "4. maximum" functions to calculate these values.
To learn more about the calculator instructions for finding maximums or minimums, select the following link:
Video Lesson
For a video lesson on using a graphing calculator to graph polynomials, select the following link:
Real Zeros
In the study of polynomial equations, the most important thing to understand is what "solution of an equation" means, because equations of higher degree allow for many solutions. The maximum number of solutions allowable is the degree of the polynomial. When a polynomial function is set equal to zero, another name for those solutions is zeros or roots.
The zeros of a polynomial are also the x-intercepts of the graph. x-intercepts can either cross the x-axis or they can just touch the x-axis without actually crossing the axis as you can see in the graphs below.
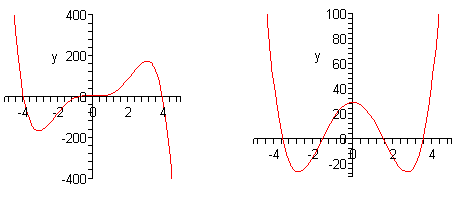
Finding Zeros
Two ways to find the zeros of the function are factoring and graphing. Factoring polynomials will be discussed in a later section, however, recall from the quadratic unit, the factored form of a function is y = (x - R1)(x - R2). To write polynomials in factored form, there will be the same number of factors as there are roots. Therefore a 4th degree polynomial might be written as P(x) = (x - R1)(x - R2)(x - R3)(x - R4).
Remember that once a polynomial is factored, setting each factor equal to 0 and solving will determine the roots or x-intercepts. When graphing, sometimes the zeros can be determined just by looking at the graph or table for the function.
Example
Find the zeros of the function: P(x) = x3 + 3x2 - 4x - 12
Step 1. Use a graphing calculator to make a graph of the function.
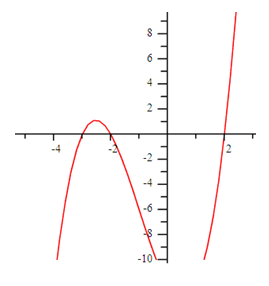
Step 2. Determine how many x-intercepts there are.
It appears there are 3 zeros or x-intercepts.
Step 3. Use the table to determine the zeros of the function.
When looking at the table, find the values of x for which y = 0. These are the x-intercepts or zeros of the function.
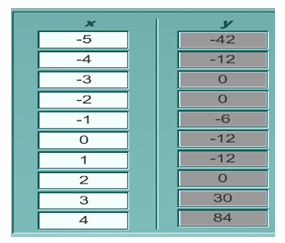
The zeros for this function are x = -3, x = -2, and x = 2.
Equations from Zeros
To write a polynomial function from its zeros, turn the zeros into factors and determine the a-value.
Example 1: Write a polynomial with roots x = 1, x = 2, and x = -3, assume the a-value is 1.
Step 1. Turn the roots into factors.
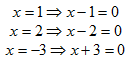
Therefore, (x - 1), (x - 2), (x + 3) are the factors.
Step 2. Write a function, include the a-value.
![]()
Example 2
Write a function in factored form that has roots r = ?1, r = 1, and r = 2, and has another point at (0, 10).
Step 1. Turn the roots into factors.
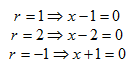
Therefore, (x - 1), (x - 2), (x + 1) are the factors.
Step 2. Write a function, include the a-value.
![]()
Step 3. Use the other point given to determine the a-value.
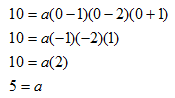
Step 4. Write the function rule.
![]()
Important Rules
There are three important theorems to remember with polynomials:
1. A polynomial of nth degree can be factored into n linear factors.
2. A polynomial equation of degree n has exactly n roots. These will be the total of real and non-real roots.
3. If (x ? r) is a factor of a polynomial, then x = r is a root of the associated polynomial equation.
Examples
Example 1 In the polynomial, P(x) = x4 - 4x3 -2x + 3, how many roots are possible?
There will be a total of 4 roots. How to determine the number of real and non-real roots is a discussion for a later course.
Example 2 How many linear factors can the polynomial, P(x) = x3 - 3x2 - 2x + 6, have?
At most, the polynomial will have three linear factors.
*Note: This polynomial can be factored to ![]() - three linear factors.
- three linear factors.
Using a Calculator
To learn how to graph polynomials and determine their number of real zeros with a graphing calculator, select the following link:
For more information on finding roots of polynomials, select the following link:
Practice
Modeling Polynomials Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Modeling Polynomials Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser
Guided Practice
For guided practice on characteristics of polynomial graphs, complete problems #15 - 27 by selecting the following link:
Practice
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser
Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Algebra Lab, "Maximum and Minimum Values of polynomials." http://www.algebralab.org/lessons/lesson.aspx?file=Algebra_poly_maxmin.xml (accessed 08/10/10).
Analyze Math, "Even and Odd Functions." http://www.analyzemath.com/function/even_odd.html (accessed 08/15/10).
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
"End Behavior and Finding Complete Graphs of Polynomial Functions." http://math.la.asu.edu/~abramson/Lessons_Poly_EndBeh_Complete.htm (accessed 08/12/10).
"Finding Minimums and Maximums." http://people.richland.edu/ james/ti82/minmax/ (accessed 08/10/10).
Holt, Rinehart & Winston, "Graphing Higher-Degree Polynomials on a Calculator." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=7126/7126.xml (accessed 9/7/2010).
Holt, Rinehart & Winston, "Graphing Polynomials." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg2/player.html?contentSrc=8167/8167.xml (accessed 9/7/2010).
Hot Math, "Practice Problems." http://hotmath.com/help/ gt/ genericalg2/section_6_4.html (accessed 08/10/10).
Interactive Mathematics, "Polynomial Functions and Equations." http://www.intmath.com/EqnsHiDe/1_Polynomials.php (accessed 8/13/10).
Paul's Online Notes, "Algebra: Graphing Polynomials." http://tutorial.math.lamar.edu/Classes/Alg/GraphingPolynomials.aspx (accessed 08/10/10).
Purple Math, "Polynomial Graphs: End Behavior." http://www.purplemath.com/modules/polyends.htm (accessed 08/10/10).
Texas Instruments, "The quest for Roots of Higher Order Equations." http://education.ti.com/educationportal/activityexchange/Activity.do?cid=US&aId=6427 (accessed 08/21/2010).
University of Saskatchewan, "Sketches of Polynomials." http://math.usask.ca/emr/examples/grpo_eg4.html (accessed 08/10/10).