Factoring Special Patterns
| Site: | St. Louis |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Factoring Special Patterns |
| Printed by: | Guest user |
| Date: | Sunday, November 30, 2025, 7:06 AM |
Description
Factoring Special Patterns
Introduction
Sum & Difference of Cubes
Sum of Cubes:x3 + y3 = (x + y) (x2 - xy + y2)
Difference of Cubes:x3 - y3 = (x - y) (x2 + xy + y2)
Example Factor the following polynomial: 64x3 + 125.
Step 1. Determine if you have a sum or difference of two cubes.
64x3 is (4x)3 and 125 is 53, so this is a sum of cubes.
Step 2. Use the pattern to factor.
(x + y) (x2 - xy + y2); x = 4x and y = 5
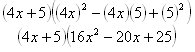
General Rules for Factoring
- Factor out the greatest common factor first, if possible.
- If the polynomial to be factored is a binomial, then it may be a difference of two squares, or a sum or difference of two cubes (remember that a sum of two squares does not factor).
- If the polynomial to be factored is a trinomial, then:
- the polynomial may be a perfect square if two of the three terms are perfect squares.
- the polynomial may be one of the general forms.
- If the polynomial to be factored consists of four or more terms, try factoring by grouping.
- Check if any of the factors can be factored further and do so when necessary.
- Finally, check the factoring by multiplying the factors to determine if they equal the original polynomial.
Practice
Answer Key
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Hensley, Patrica. "Genera; Advice for Factoring Polynomials." http://one.nettrekker.com/goExternal?np=/external.ftl&pp=/error.ftl&evlCode=35064&productName=school&HOMEPAGE=H (accessed 08/13/10).
Interactive Math, "Sum and Differences of Cubes." http://www.intmath.com/ FactFrac/4_SDCub.php (accessed 08/13/10).