Fractional Exponents
| Site: | St. Louis |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Fractional Exponents |
| Printed by: | Guest user |
| Date: | Thursday, January 29, 2026, 12:23 AM |
Description
Introduction
The last area of power functions to be addressed is the case of a fractional exponent. In order to express a radical expression without a radical sign, fractional (or rational) exponents are used. Some radical expressions and their equivalent rational exponent expressions are below:
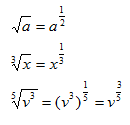
Fractional exponents are much easier to manipulate in solving equations than radicals, because all of the exponent rules apply to rational exponents. In general, roots can be written with fractional exponents in the following manner:
Roots as Fractional Exponents:![]()
The value on the radical becomes the denominator of the fractional exponent. The exponent on the value beneath the radical becomes the numerator of the fractional exponent.
Examples
Example 1 Simplify ![]()
Apply the Product of a Power Rule.
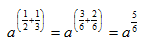
Example 2 Simplify ![]() .
.
Apply the Power of a Power Rule.
![]()
More Examples
Example 3 Simplify ![]() .
.
Apply the Quotient of a Power Rule
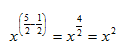
Example 4 Simplify ![]() .
.
Apply the Power of a Quotient Rule.
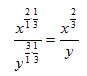
Video Lessons
To learn how to simplify expressions involving fractional exponents, select the following links:
Guided Practice
To solidify your understanding of rational exponents, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Fractional Exponents Worksheet
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Fractional Exponents Answer Key
*Note:If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Gloag, Andrew & Anne. "Exponential Functions." http://www.ck12.org/flexr/chapter/4478 (accessed August 31, 2010)
Holt, Rinehart, & Winston. "Exponents and Roots." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/
alg2_ch08_06_homeworkhelp.html (accessed September 1, 2010).