Multiplying & Dividing
| Site: | St. Louis |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Multiplying & Dividing |
| Printed by: | Guest user |
| Date: | Thursday, November 21, 2024, 12:22 PM |
Description
Multiplying
In order to multiply two or more radical expressions of the same degree, the expressions under the radical sign can be multiplied.
Product Property of Roots:
Example 1 What is the product of 
?
Step 1. Verify the degree of the radicals are the same.
Both terms have a degree of 3.
Step 2. Use the Product Property of Roots to multiply the terms.
Example 2 What is the product of 
? Assume all variables are positive.
Step 1. Verify the degree of the radicals are the same.
Two terms have a degree of two and can be multiplied, the term with degree 3 will stay the same.
Step 2. Use the Product Property of Roots to multiply the terms with the same degree.
Examples with Simplifying
Example 3 Simplify 
, assume all variables are positive.
Step 1. Verify the degree of the radicals are the same.
Both terms have a degree of 3.
Step 2. Use the Product Property of Roots to multiply the terms.
Step 3. Simplify.
Example 4 Simplify 
, assume all variables are positive.
Step 1. Verify the degree of the radicals are the same.
Two terms have a degree of two and can be multiplied, the term with degree 4 will stay the same.
Step 2. Use the Product Property of Roots to multiply the terms with the same degree.
Step 3. Simplify.
Video Lesson
To learn how to multiply radical expressions, select the following link:
Dividing
In order to divide radical expressions of the same degree, the expressions under the radical sign can be divided.
Quotient Property of Roots: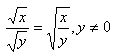
Example 1 What is the quotient of 
?
Step 1. Verify the degree of the radicals are the same.
Both terms have a degree of 3.
Step 2. Use the Quotient Property of Roots to divide the terms.
Examples with Simplifying
Example 2 Simplify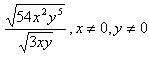 
.
Step 1. Verify the degree of the radicals are the same.
Both terms have a degree of 2.
Step 2. Use the Quotient Property of Roots to divide the terms.
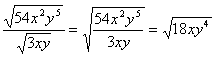
Step 3. Simplify.
Example 3 Simplify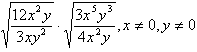 
.
Step 1. Verify the degree of the radicals are the same.
Both terms have a degree of 2.
Step 2. Use properties of Roots to create one radical expression (there are many different ways to approach this problem).
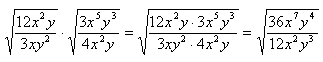
Step 3. Simplify.
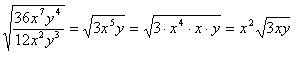
Rationalizing the Denominator
Sometimes it is desirable to find an equivalent radical expression that does not contain radicals in the denominator. This process is called rationalizing the denominator. The goal is to make sure there are no radicals left in the denominator of the fraction. In order to do this, multiply the fraction by a fraction equal to one.
In order to understand the process of rationalizing a denominator, please select the following link to an on-line lesson and examples:
Rationalizing the Denominator Lesson
To learn how to rationalize the denominator, select the following link:
Rationalizing the Denominator Video Lesson
Guided Practice
To solidify your understanding of simplifying radicals, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Practice
Multiplying and Dividing Radicals Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Multiplying and Dividing Radicals Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
DeMarr, Elizabeth. "Rationalizing Denominators with Radicals." http://www.regentsprep.org/Regents/math/algtrig/ATO3/rdlesson.htm (accessed 1/8/2011).
HelpAlgebra.com, "How to Rationalize the Denominator." http://www.helpalgebra.com/articles/rationalizedenominator.htm (accessed 1/8/2011).
Holt, Reinhart & Winston, "Exponential and Radical Functions ." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch11_08_homeworkhelp.html (accessed 1/8/2011).
Holt, Reinhart & Winston, "Multiply and Divide Radical Expressions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg1/player.html?contentSrc=6395/6395.xml (accessed 1/8/2011).
Holt, Reinhart & Winston, "Multiply and Divide Radical Expressions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg1/player.html?contentSrc=7877/7877.xml (accessed 1/8/2011).